Launching Math Lessons
Proven Practices
“No other decision that teachers make has greater impact on students’ opportunities to learn and on their perceptions about what mathematics is than the selection or creation of the tasks with which the teacher engages the students in studying mathematics. Here, the teacher is the architect, the designer of the curriculum.”
- Reys & Long 1995
Tried & True Practice - by Dr. Carrie Zielinski
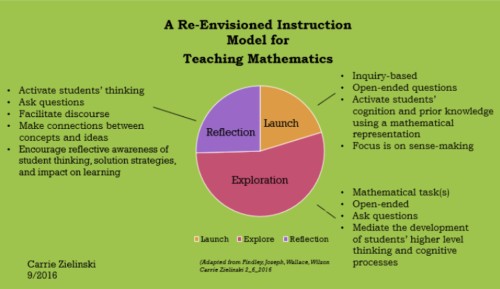
Launching a Mathematics Lesson
Begin with Questions
Description of the launch for a lesson
A launch is a brief (5 – 15 minutes) inquiry-based investigation. Grounded in learning theory, the launch invokes and makes visible students’ existing schema relative to the goals of a lesson. An effective launch acknowledges learners as active participants, assists them in connecting prior knowledge to new insights, and provides all students access to the content and concepts of a lesson.
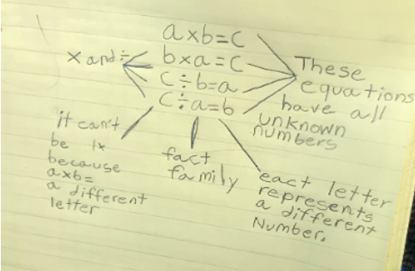
To effectively launch a mathematics lesson, the teacher poses a mathematical representation such as a model, a story problem, a question, or claim. The representation should provoke students’ curiosities, as well as activate their perceptions of significant or informative mathematical details related to the intended goals of the lesson (Learner & Johns, 2012).
Once presented, students need time to observe, analyze, and make sense of the mathematical representation for themselves. (Garner, 2007). Thus, teachers do not tell students what to notice, nor should they anticipate a specific response. Rather, teachers use open-ended questions such as: “What sense can you make of this?” or, “What do you notice?” or, “What do you wonder?” Open-ended questions unlock cognitive space and emboldens students’ initial associations, impressions, and references.
Recorded Observations in Mathematician’s Notebooks
Once students observe and make sense of the representation, they are encouraged to record their observations, ideas, and impressions within their mathematician’s notebooks.
As students record their descriptions, wonderings, and own models, the teacher circulates around the room and invites specific learners to publicly share their thinking. Students are invited to place their own representations, strategies, or models under a document camera and vocally share and physically model their ideas for others.
Alternatively, students may share their interpretations or observations whereby the teacher records, verbatim, students’ words onto large chart paper, white board, or SMART Board. Even students’ non-mathematical observations and misconceptions are shared because they provide rich opportunities for learning and discussion. Such actions allow all to hear, see, make sense of, access, critique and review classmates’ perceptions, strategies, and models. In all cases, however, artful scaffolding of students’ work supports struggling learners, as well as advanced learners contributing to the entire learning community.
Sharing Their Observations with the Class
The resulting anchor chart of students’ “noticings” offers invaluable information for teacher and students alike. Students’ shared ideas scaffold fellow classmates’ opportunities for enhanced group learning. Student descriptions reflect their current understandings whereby teachers make decisions regarding next steps for instruction. Finally, students’ posted information offers the entire group a reference point or “collective memory” (e.g., pre-assessment data) to reference during the remaining segments of the lesson.
Additional options for launching a lesson include sharing students’ previous work or intentionally selecting student work samples that are mathematically correct or incorrect. Once again, the teacher asks students to closely examine and make sense of classmates’ strategies, representation(s), misconceptions, or generalizations. Asking students to notice important mathematical details, while making connections to what they already know, further support students’ investigations, engagement, and refinement of concepts central to learning mathematics.
In a “Nutshell”, the Launch:
- Is inquiry-based.
- Invites students to make sense of a mathematical representation.
- Provides all students access to the content of a lesson.
- Actively engages students with the concepts of a lesson.
- Supports students accessing prior knowledge by placing it into short-term and working memories.
- Offers opportunities for students to build upon each other’s ideas, to validate one another’s thinking, and/or correct misconceptions.
- Provides formative assessment data for teacher and for students.
Ideas to Consider When Selecting the Mathematical Representation:
- What mathematical ideas (conceptual and procedural) do you want your students to understand, know, and do by the end of the lesson?
- How might students interpret the representation(s) you have selected?
- In what ways will the selected representation build upon students’ existing schema?
- How will you introduce students to the task or representation, provide access to all, and NOT undermine student thinking?
- What questions will you ask to assist students accessing their prior knowledge?
- What possible mathematical misconceptions might arise?
Questions to pose during the enactment of the Launch**:
- What do you notice? What sense can you make of this?
- What might this statement or question ask you to think about? How do you know?
- What mathematical ideas comes to mind?
- How might this representation connect to concepts we’ve already studied?
- What patterns or structure do you see within this mathematical representation?
- Where might you have seen this before?
References
**Garner, B. K. (2007). Getting to got it: Helping struggling students learn how to learn. Alexandria, VA: Association for Supervision and Curriculum Development.
Learner, J. W., & Johns, B. H. (2012). Learning Disabilities and Related Mild Disabilities: Teaching Strategies and New Directions. Belmont, CA: Wadsworth Cengage Learning.
Monroe Public Schools: Math Workshop Model. Monroe, MI.
Reys, B.J., & Long, V. (1995). Teacher as architect of mathematical tasks. Teaching Children Mathematics, 1(5), 296-299.
**Smith, M., Bill, V., & Hughes, E. (2008). Thinking through a Lesson: Successfully Implementing High-Level Tasks. Mathematics Teaching in the Middle School 14(3), 132-138.
Zielinski, C. D. (2018). A re-envisioned instruction model: Minimizing students’ learning difficulties in mathematics. [Doctoral dissertation, University of Michigan – Dearborn.]